Február 24: szökőnap



Sokan emlékezhetnek még a klasszikus matematikai fejtörőre: negyven éve született, de csak tízszer volt születésnapja. Mikor született az illető? Február 29-én, szökőnapon – válaszolta sok kisdiák lelkesen, a matematikatanárok többsége pedig bólogatott hozzá. A megoldás viszont helytelen. A szökőnap ugyanis négyévente február 24-e!
Ilyenkor ezen a napon nem ünneplünk semmilyen névnapot, az eredetileg február 24-28-a közé eső névnapok pedig egy nappal tolódnak. De aki szökőévben született Elemér napján, február 29-én, nyugodtan ünnepelheti születésnapját a többi évben február 28-án. Kellemetlenebb a helyzete annak, aki szökőévben született február 24-én, szökőnapon, neki valóban csak négyévente van születésnapja. Az eltolás mindenkit érint, aki február 24-28 között született, nekik elméletileg négy évente illene egy nappal elcsúsztatni születésnapjuk ünneplését.
Julius Caesar, a reformer
A szökőévek és a szökőnap tekintetében a rómaiaknál vágjunk bele a kalendárium rejtelmeibe. A rómaiak kezdetben 10 hónapból álló, 29-30 napos éveket használtak, később 12 hónapra bővítették a naptárt. A 365 és ¼ napos luniszolár évet
Julius Ceasar
vezeti be. Caesar ie. 46-ban elrendelte, hogy az év 365 napból álljon a hónapoknak ma is szokásos hosszával, de az ¼ nap miatt minden negyedik évben a február 23-a után egy napot iktassanak közbe. A szökőévet bisextilisnek nevezték, mert február 23-a a hatodik nap volt márciustól számítva, és a reform keretében tulajdonképpen ezt a napot kettőzték meg. Később ezt a „juliáni” naptárt a keresztények is átvették.
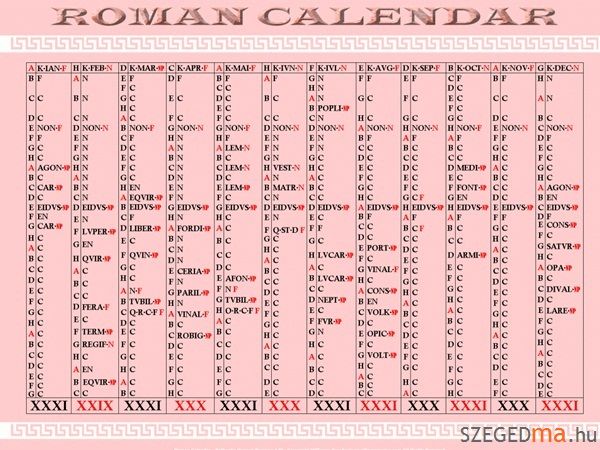
A római naptár, az őrület határán
A rómaiak Julius Caesar előtt 355 napos évet használtak, 29 és 30 napos hónapokkal, és nem a hónap első napjától az utolsóig sorszámozták napjaikat, hanem volt három fix nap, amelyekhez képest relatív számozást használtak. Calendae volt a hó első napja – innen ered a kalendárium szavunk is –, Idus volt a hó közepe – március, május, július és október 15-e – egyébként 13-a volt a Nonae Idus előtti nyolcadik nap. Ezek után szeptember hó negyedik napja volt „nóna másodikja” (két nappal nóna előtt, nónát elsőnek véve), kilencedik napja volt „idus ötödikje” (öt nappal idus előtt, idust elsőnek véve) és huszonnegyedik napja volt (október) „calendaejának hetedikje” (mert szeptember 29 napos volt). Az újesztendő így március calendaejára esett. A „szökődolgot” időnként szökőhónappal (intercalaris) korrigálták az újév előtt, amikor már nagyon felgyűlt a lunáris év és szoláris év közötti (a Hold, illetve a Nap alapján számolt év) eltérés, amit nyolc évenként háromszor ragasztottak hozzá. Az igazi zavart a római gondolkodás különös logikája okozza, mivel a napokat nem a hónap elejétől előre, hanem a következő hónap első napjától visszafelé számolták. Míg mi azt mondjuk, hogy 24 nap telt el a februárból, ők azt mondták, hogy még hat nap van hátra március elsejéig. Amíg mi azt számoljuk, ami elmúlt, ők azt számolták, hogy hány napnak kell eltelnie még a következő hónap első napjáig. Julius Caesar megbízására – hogy rendezze a naptárkérdést –
Szoszigenész
elkészítette a ma juliánus naptárként tisztelt rendszert, amely már szökőnapos volt. Amikor a császár elé terjesztette munkáját, az rendeletben hirdette ki azt. Ebben már az szerepelt, hogy március calendaejának hatodikját duplázni kell (bissextile). Tehát szökőévben az ilyen napból kettő volt, amelyből a visszafelé számlálás miatt az elsőt tekintették járuléknak, azaz szökőnapnak.
A Gergely-naptár

A Föld nap körüli pályája azonban nem 365 ¼ nap, hanem 365 nap 5 óra 48 perc, 46,17 másodperc, ezért a naptár és a valós idő között napi 11 perc eltérés alakult ki. Ez 129 év alatt egy teljes napot jelentett, a XVI. századra pedig már 13 nap „gyűlt össze”.
XIII. Gergely pápa
ezért 1582-ben elrendelte, hogy október 4-e után 15-ét írjanak, továbbá úgy döntöttek, hogy minden negyedik év, tehát azok az évek, amelyek évszáma néggyel osztható, 366 napos szökőév legyen, de a százados évek, 1600, 1700 közül csak azok, melyek 400-zal oszthatók. Tehát 1600 szökőév, de ezt követően 1700, 1800 és 1900 közönséges évek maradtak. Magyarország 1587-ben fogadta el a Gergely-naptárt, amikor is 1587. október 21. szerda után, november 1. csütörtök következett, és ezzel szinkronba kerültünk a legtöbb európai országgal. Ez a naptár meghatározott években a 28 napos február hónaphoz egy plusz napot ad, így az a szökőévben 29 napos lesz.
Mely évek a szökőévek?
Szökőévek a következők: minden néggyel osztható év, kivéve a százzal is oszthatókat. Szökőévek viszont a 400-zal osztható évek. Vagyis a százasra végződő évek közül csak azok szökőévek, amelyek 400-al is oszthatók. Ez alapján tehát szökőév volt 1988, 1992, 1996. Nem szökőév 1700, 1800, 1900, 2100, és 2200. Viszont szökőévek az alábbi esztendők: 1600, 2000 és 2400. A Gergely-naptárban így minden 400 évre 97 szökőév jut. A Gergely-naptár alapján tehát az év átlagos hossza 365,2425 nap. A csillagászati év hossza viszont 365,2424 nap. A kettő különbségéből fakadó eltérés alig több mint 0,0001 nap. Ez azt jelenti, hogy a Gergely-naptár nagyjából 8000 évente marad el 1 nappal a csillagászati naptár mögött. Johannes Herschel (1792–1871) javasolta – másokkal egyetemben – hogy a pontosság kedvéért minden 4000. év legyen kivételesen nem szökőév, azonban ez a javaslat nem élvez támogatást, főként annak ritka alkalmazása miatt.
De miért épp február 24-e?
Hogy miért éppen ide suvasztották a szökőnapot? Részben azért, mert a hagyomány ezt követelte, mivel az intercalaris hónapnak is ez volt a helye, nem pedig február és március között, másrészt a calendae adóügyi szempontból kiemelkedő nap volt, s emiatt a naptárügyi kacskaringókat távol akarták ettől tartani.
Február 24-e az a nap, amelyet a liturgikus naptárak, így a magyar naptárral kiegészített római naptár szerint is szökőévben „kétszer kell mondani” – azaz írni, és amelyről a régi, a II. Vatikáni Zsinat előtti liturgikus naptárban Mátyás napját február 25-re tették. Ez volt „Mátyás ugrása”. Igaz ugyan, hogy a mai liturgikus naptárban már nincs ilyen, négyévenként megismétlődő eseti áttétel, a szökőnap tekintetében nincs változás, az továbbra is február 24., de már a Mátyás-nappal együtt, ezért az egyszerűbb egyházi naptárakban már nem is jelzik. Talán éppen az a baj, hogy a zsinat itt egy „meggondolatlan” lépést tett: a „Mátyás ugrása” elhagyása azt a látszatot kelti, hogy a szökőnapnak nincs igazi jelentősége. Ha ugyanarra a napra esik a Mátyás-nap, úgy talán nem is ez szökőnap, hanem a közönséges évekhez képest egy nappal meghosszabbított február utolsó napja. Így kerülhet még az egyházi kiadású kalendáriumokba is szökőnapként február 29. A február szökőhónap jellege ugyanis nem egy toldaléknap egyszerű hozzáadását jelenti, nem így hosszabbodik meg a hónap, hanem a 24. nap megduplázásával, amivel a hónap következő napjai eggyel előre lépnek a hetinapok sorában. Ennek pedig a régi római naptárra visszavezethető naptártörténeti okai vannak, amelyet a zsinat előtti egyházi gyakorlattal együtt mi is örököltünk. A XX. századi naptárreform törekvések során létrejött ugyan néhány, a naptári évet egyenletesebbé tevő öröknaptár, de egyikük sem tudta elkerülni névtelen napok beiktatását, amelyekkel megszakította volna a hét napjainak a biblikus idők óta szakadatlan sorozatát.
Hiányos naptárkultúra
A mai naptárkultúránk sajnos más szempontból is hiányos. A napjainkban kiadott igen sokféle naptár, évkönyv, almanach szép megjelenése ellenére is már szinte pusztán csak a névnapok jegyzéke. De annak is pontatlan, mert a polgári naptárakban a katolikus Magyarországon csak a protestáns névnapokat közlik, így a katolikus misekönyvekben az egyes szentek ünnep-, illetve emléknapjai nem esnek egybe a polgári naptárakban szereplő névnapokkal. Pedig a párhuzamos naptárakat már a XX. század elején is használták: a kalendárium jellegű kiadványokban külön hasábokban szerepeltették a katolikus, a görög katolikus, a protestáns, és a zsidó ünnepeket, illetve névnapokat. A kiadványok elején ott szerepeltek az adott év naptárszerkezeti megkülönböztetésére alkalmas elemek is: • az év típusát jelző vasárnapbetű (összesen 14 évtípus lehetséges) • az epacta (a Hold újév napi kora) • az indictio (a régi római adófizetési év aktuális periódusa) • az aranyszám (amely megmondja, hogy a 19 éves holdciklus – a Meton-ciklus – hányadik éve az adott esztendő • a napkör (a hetinapok köre, amely megmondja, hogy a napok folyamatos vándorlásának 28 éves ciklusában hányadik évben járunk) • a napéjegyenlőségek és napfordulók pontos dátuma és időpontja • a holdfázisok • a húsvéti Hold dátuma (a tavaszi napéjegyenlőséget követő első holdtölte) • az ezt követő vasárnapon: a húsvét dátuma Az igényesebb kalendáriumokban ezeken kívül még megtalálhatók a bizánci, a mohamedán, a zsidó, és az ab Urbe condita, azaz a Város (Róma) alapításától számított időszámítás megfelelő évszámai is. Forrás:
Magyar Csillagászati Egyesület
Schalk Gyula: